Sep 12, 2020 Algorithms and Data Structures Cheatsheet We summarize the performance characteristics of classic algorithms and data structures for sorting, priority queues, symbol tables, and graph processing. Big o cheatsheet with complexities chart Big o complete Graph!Bigo graph1 Legend!legend3!Big o cheatsheet2!DS chart4!Searching chart5 Sorting Algorithms chart!sorting chart6!Heaps chart7!graphs chart8. HackerEarth is a global.
- Fantasy Football Cheat Sheet
- Algorithm Complexity Cheat Sheet Pdf
- Big-o Algorithm Complexity Cheat Sheet Pdf
When measuring the efficiency of an algorithm, we usually take into account the time and space complexity. In this article, we will glimpse those factors on some sorting algorithms and data structures, also we take a look at the growth rate of those operations.
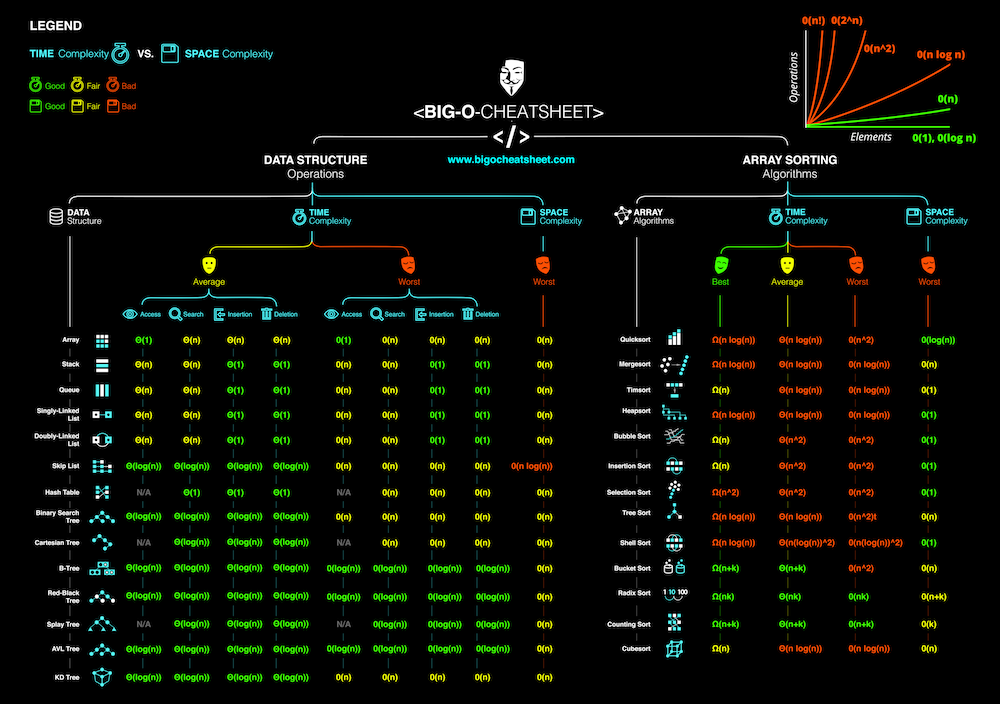
Big-O Complexity Chart
First, we consider the growth rate of some familiar operations, based on this chart, we can visualize the difference of an algorithm with O(1) when compared with O(n2). As the input larger and larger, the growth rate of some operations stays steady, but some grow further as a straight line, some operations in the rest part grow as exponential, quadratic, factorial.
Sorting Algorithms
In order to have a good comparison between different algorithms we can compare based on the resources it uses: how much time it needs to complete, how much memory it uses to solve a problem or how many operations it must do in order to solve the problem:
- Time efficiency: a measure of the amount of time an algorithm takes to solve a problem.
- Space efficiency: a measure of the amount of memory an algorithm needs to solve a problem.
- Complexity theory: a study of algorithm performance based on cost functions of statement counts.
| Sorting Algorithms | Space Complexity | Time Complexity | ||
| Worst case | Best case | Average case | Worst case | |
Bubble Sort | O(1) | O(n) | O(n2) | O(n2) |
| Heapsort | O(1) | O(n log n) | O(n log n) | O(n log n) |
| Insertion Sort | O(1) | O(n) | O(n2) | O(n2) |
| Mergesort | O(n) | O(n log n) | O(n log n) | O(n log n) |
| Quicksort | O(log n) | O(n log n) | O(n log n) | O(n log n) |
| Selection Sort | O(1) | O(n2) | O(n2) | O(n2) |
| ShellSort | O(1) | O(n) | O(n log n2) | O(n log n2) |
| Smooth Sort | O(1) | O(n) | O(n log n) | O(n log n) |
| Tree Sort | O(n) | O(n log n) | O(n log n) | O(n2) |
| Counting Sort | O(k) | O(n + k) | O(n + k) | O(n + k) |
| Cubesort | O(n) | O(n) | O(n log n) | O(n log n) |
Data Structure Operations
In this chart, we consult some popular data structures such as Array, Binary Tree, Linked-List with 3 operations Search, Insert and Delete.
| Data Structures | Average Case | Worst Case | ||||
| Search | Insert | Delete | Search | Insert | Delete | |
| Array | O(n) | N/A | N/A | O(n) | N/A | N/A |
| AVL Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| B-Tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| Binary SearchTree | O(log n) | O(log n) | O(log n) | O(n) | O(n) | O(n) |
| Doubly Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Hash table | O(1) | O(1) | O(1) | O(n) | O(n) | O(n) |
| Linked List | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
| Red-Black tree | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) | O(log n) |
| Sorted Array | O(log n) | O(n) | O(n) | O(log n) | O(n) | O(n) |
| Stack | O(n) | O(1) | O(1) | O(n) | O(1) | O(1) |
Growth of Functions
The order of growth of the running time of an algorithm gives a simple characterization of the algorithm’s efficiency and also allows us to compare the relative performance of alternative algorithms.
Below we have the function n f(n) with n as an input, and beside it we have some operations which take input n and return the total time to calculate some specific inputs.
| n f(n) | log n | n | n log n | n2 | 2n | n! |
|---|---|---|---|---|---|---|
| 10 | 0.003ns | 0.01ns | 0.033ns | 0.1ns | 1ns | 3.65ms |
| 20 | 0.004ns | 0.02ns | 0.086ns | 0.4ns | 1ms | 77years |
| 30 | 0.005ns | 0.03ns | 0.147ns | 0.9ns | 1sec | 8.4×1015yrs |
| 40 | 0.005ns | 0.04ns | 0.213ns | 1.6ns | 18.3min | — |
| 50 | 0.006ns | 0.05ns | 0.282ns | 2.5ns | 13days | — |
| 100 | 0.07 | 0.1ns | 0.644ns | 0.10ns | 4×1013yrs | — |
| 1,000 | 0.010ns | 1.00ns | 9.966ns | 1ms | — | — |
| 10,000 | 0.013ns | 10ns | 130ns | 100ms | — | — |
| 100,000 | 0.017ns | 0.10ms | 1.67ms | 10sec | — | — |
| 1’000,000 | 0.020ns | 1ms | 19.93ms | 16.7min | — | — |
| 10’000,000 | 0.023ns | 0.01sec | 0.23ms | 1.16days | — | — |
| 100’000,000 | 0.027ns | 0.10sec | 2.66sec | 115.7days | — | — |
| 1,000’000,000 | 0.030ns | 1sec | 29.90sec | 31.7 years | — | — |
We summarize the performance characteristics of classic algorithms anddata structures for sorting, priority queues, symbol tables, and graph processing.
We also summarize some of the mathematics useful in the analysis of algorithms, including commonly encountered functions;useful formulas and appoximations; properties of logarithms;asymptotic notations; and solutions to divide-and-conquer recurrences.

Sorting.
The table below summarizes the number of compares for a variety of sortingalgorithms, as implemented in this textbook.It includes leading constants but ignores lower-order terms.| ALGORITHM | CODE | STABLE | BEST | AVERAGE | WORST | REMARKS | |
|---|---|---|---|---|---|---|---|
| selection sort | Selection.java | ✔ | ½ n 2 | ½ n 2 | ½ n 2 | n exchanges; quadratic in best case | |
| insertion sort | Insertion.java | ✔ | ✔ | n | ¼ n 2 | ½ n 2 | use for small or partially-sorted arrays |
| bubble sort | Bubble.java | ✔ | ✔ | n | ½ n 2 | ½ n 2 | rarely useful; use insertion sort instead |
| shellsort | Shell.java | ✔ | n log3n | unknown | c n 3/2 | tight code; subquadratic | |
| mergesort | Merge.java | ✔ | ½ n lg n | n lg n | n lg n | n log n guarantee; stable | |
| quicksort | Quick.java | ✔ | n lg n | 2 n ln n | ½ n 2 | n log n probabilistic guarantee; fastest in practice | |
| heapsort | Heap.java | ✔ | n† | 2 n lg n | 2 n lg n | n log n guarantee; in place | |
| †n lg n if all keys are distinct | |||||||
Fantasy Football Cheat Sheet
Priority queues.
The table below summarizes the order of growth of the running time ofoperations for a variety of priority queues, as implemented in this textbook.It ignores leading constants and lower-order terms.Except as noted, all running times are worst-case running times.| DATA STRUCTURE | CODE | INSERT | MIN | DELETE | MERGE | ||
|---|---|---|---|---|---|---|---|
| array | BruteIndexMinPQ.java | 1 | n | n | 1 | 1 | n |
| binary heap | IndexMinPQ.java | log n | log n | 1 | log n | log n | n |
| d-way heap | IndexMultiwayMinPQ.java | logdn | d logdn | 1 | logdn | d logdn | n |
| binomial heap | IndexBinomialMinPQ.java | 1 | log n | 1 | log n | log n | log n |
| Fibonacci heap | IndexFibonacciMinPQ.java | 1 | log n† | 1 | 1 † | log n† | 1 |
| † amortized guarantee | |||||||
Symbol tables.
The table below summarizes the order of growth of the running time ofoperations for a variety of symbol tables, as implemented in this textbook.It ignores leading constants and lower-order terms.| worst case | average case | ||||||
|---|---|---|---|---|---|---|---|
| DATA STRUCTURE | CODE | SEARCH | INSERT | DELETE | SEARCH | INSERT | DELETE |
| sequential search (in an unordered list) | SequentialSearchST.java | n | n | n | n | n | n |
| binary search (in a sorted array) | BinarySearchST.java | log n | n | n | log n | n | n |
| binary search tree (unbalanced) | BST.java | n | n | n | log n | log n | sqrt(n) |
| red-black BST (left-leaning) | RedBlackBST.java | log n | log n | log n | log n | log n | log n |
| AVL | AVLTreeST.java | log n | log n | log n | log n | log n | log n |
| hash table (separate-chaining) | SeparateChainingHashST.java | n | n | n | 1 † | 1 † | 1 † |
| hash table (linear-probing) | LinearProbingHashST.java | n | n | n | 1 † | 1 † | 1 † |
| † uniform hashing assumption | |||||||
Graph processing.
The table below summarizes the order of growth of the worst-case running time and memory usage (beyond the memory for the graph itself)for a variety of graph-processing problems, as implemented in this textbook.It ignores leading constants and lower-order terms.All running times are worst-case running times.
Itools pro for mac os x torrent.
| PROBLEM | ALGORITHM | CODE | TIME | SPACE |
|---|---|---|---|---|
| path | DFS | DepthFirstPaths.java | E + V | V |
| shortest path (fewest edges) | BFS | BreadthFirstPaths.java | E + V | V |
| cycle | DFS | Cycle.java | E + V | V |
| directed path | DFS | DepthFirstDirectedPaths.java | E + V | V |
| shortest directed path (fewest edges) | BFS | BreadthFirstDirectedPaths.java | E + V | V |
| directed cycle | DFS | DirectedCycle.java | E + V | V |
| topological sort | DFS | Topological.java | E + V | V |
| bipartiteness / odd cycle | DFS | Bipartite.java | E + V | V |
| connected components | DFS | CC.java | E + V | V |
| strong components | Kosaraju–Sharir | KosarajuSharirSCC.java | E + V | V |
| strong components | Tarjan | TarjanSCC.java | E + V | V |
| strong components | Gabow | GabowSCC.java | E + V | V |
| Eulerian cycle | DFS | EulerianCycle.java | E + V | E + V |
| directed Eulerian cycle | DFS | DirectedEulerianCycle.java | E + V | V |
| transitive closure | DFS | TransitiveClosure.java | V (E + V) | V 2 |
| minimum spanning tree | Kruskal | KruskalMST.java | E log E | E + V |
| minimum spanning tree | Prim | PrimMST.java | E log V | V |
| minimum spanning tree | Boruvka | BoruvkaMST.java | E log V | V |
| shortest paths (nonnegative weights) | Dijkstra | DijkstraSP.java | E log V | V |
| shortest paths (no negative cycles) | Bellman–Ford | BellmanFordSP.java | V (V + E) | V |
| shortest paths (no cycles) | topological sort | AcyclicSP.java | V + E | V |
| all-pairs shortest paths | Floyd–Warshall | FloydWarshall.java | V 3 | V 2 |
| maxflow–mincut | Ford–Fulkerson | FordFulkerson.java | EV (E + V) | V |
| bipartite matching | Hopcroft–Karp | HopcroftKarp.java | V ½ (E + V) | V |
| assignment problem | successive shortest paths | AssignmentProblem.java | n 3 log n | n 2 |

Commonly encountered functions.
Here are some functions that are commonly encounteredwhen analyzing algorithms.| FUNCTION | NOTATION | DEFINITION |
|---|---|---|
| floor | ( lfloor x rfloor ) | greatest integer (; le ; x) |
| ceiling | ( lceil x rceil ) | smallest integer (; ge ; x) |
| binary logarithm | ( lg x) or (log_2 x) | (y) such that (2^{,y} = x) |
| natural logarithm | ( ln x) or (log_e x ) | (y) such that (e^{,y} = x) |
| common logarithm | ( log_{10} x ) | (y) such that (10^{,y} = x) |
| iterated binary logarithm | ( lg^* x ) | (0) if (x le 1;; 1 + lg^*(lg x)) otherwise |
| harmonic number | ( H_n ) | (1 + 1/2 + 1/3 + ldots + 1/n) |
| factorial | ( n! ) | (1 times 2 times 3 times ldots times n) |
| binomial coefficient | ( n choose k ) | ( frac{n!}{k! ; (n-k)!}) |
Useful formulas and approximations.
Here are some useful formulas for approximations that are widely used in the analysis of algorithms.- Harmonic sum: (1 + 1/2 + 1/3 + ldots + 1/n sim ln n)
- Triangular sum: (1 + 2 + 3 + ldots + n = n , (n+1) , / , 2 sim n^2 ,/, 2)
- Sum of squares: (1^2 + 2^2 + 3^2 + ldots + n^2 sim n^3 , / , 3)
- Geometric sum: If (r neq 1), then(1 + r + r^2 + r^3 + ldots + r^n = (r^{n+1} - 1) ; /; (r - 1))
- (r = 1/2): (1 + 1/2 + 1/4 + 1/8 + ldots + 1/2^n sim 2)
- (r = 2): (1 + 2 + 4 + 8 + ldots + n/2 + n = 2n - 1 sim 2n), when (n) is a power of 2
- Stirling's approximation: (lg (n!) = lg 1 + lg 2 + lg 3 + ldots + lg n sim n lg n)
- Exponential: ((1 + 1/n)^n sim e; ;;(1 - 1/n)^n sim 1 / e)
- Binomial coefficients: ({n choose k} sim n^k , / , k!) when (k) is a small constant
- Approximate sum by integral: If (f(x)) is a monotonically increasing function, then( displaystyle int_0^n f(x) ; dx ; le ; sum_{i=1}^n ; f(i) ; le ; int_1^{n+1} f(x) ; dx)
Properties of logarithms.
- Definition: (log_b a = c) means (b^c = a).We refer to (b) as the base of the logarithm.
- Special cases: (log_b b = 1,; log_b 1 = 0 )
- Inverse of exponential: (b^{log_b x} = x)
- Product: (log_b (x times y) = log_b x + log_b y )
- Division: (log_b (x div y) = log_b x - log_b y )
- Finite product: (log_b ( x_1 times x_2 times ldots times x_n) ; = ; log_b x_1 + log_b x_2 + ldots + log_b x_n)
- Changing bases: (log_b x = log_c x ; / ; log_c b )
- Rearranging exponents: (x^{log_b y} = y^{log_b x})
- Exponentiation: (log_b (x^y) = y log_b x )


Aymptotic notations: definitions.
| NAME | NOTATION | DESCRIPTION | DEFINITION |
|---|---|---|---|
| Tilde | (f(n) sim g(n); ) | (f(n)) is equal to (g(n)) asymptotically (including constant factors) | ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = 1) |
| Big Oh | (f(n)) is (O(g(n))) | (f(n)) is bounded above by (g(n)) asymptotically (ignoring constant factors) | there exist constants (c > 0) and (n_0 ge 0) such that (0 le f(n) le c cdot g(n)) forall (n ge n_0) |
| Big Omega | (f(n)) is (Omega(g(n))) | (f(n)) is bounded below by (g(n)) asymptotically (ignoring constant factors) | ( g(n) ) is (O(f(n))) |
| Big Theta | (f(n)) is (Theta(g(n))) | (f(n)) is bounded above and below by (g(n)) asymptotically (ignoring constant factors) | ( f(n) ) is both (O(g(n))) and (Omega(g(n))) |
| Little oh | (f(n)) is (o(g(n))) | (f(n)) is dominated by (g(n)) asymptotically (ignoring constant factors) | ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = 0) |
| Little omega | (f(n)) is (omega(g(n))) | (f(n)) dominates (g(n)) asymptotically (ignoring constant factors) | ( g(n) ) is (o(f(n))) |
Common orders of growth.
| NAME | NOTATION | EXAMPLE | CODE FRAGMENT |
|---|---|---|---|
| Constant | (O(1)) | array access arithmetic operation function call | |
| Logarithmic | (O(log n)) | binary search in a sorted array insert in a binary heap search in a red–black tree | |
| Linear | (O(n)) | sequential search grade-school addition BFPRT median finding | |
| Linearithmic | (O(n log n)) | mergesort heapsort fast Fourier transform | |
| Quadratic | (O(n^2)) | enumerate all pairs insertion sort grade-school multiplication | |
| Cubic | (O(n^3)) | enumerate all triples Floyd–Warshall grade-school matrix multiplication | |
| Polynomial | (O(n^c)) | ellipsoid algorithm for LP AKS primality algorithm Edmond's matching algorithm | |
| Exponential | (2^{O(n^c)}) | enumerating all subsets enumerating all permutations backtracing search |
Asymptotic notations: properties.
- Reflexivity: (f(n)) is (O(f(n))).
- Constants: If (f(n)) is (O(g(n))) and ( c > 0 ),then (c cdot f(n)) is (O(g(n)))).
- Products: If (f_1(n)) is (O(g_1(n))) and ( f_2(n) ) is (O(g_2(n)))),then (f_1(n) cdot f_2(n)) is (O(g_1(n) cdot g_2(n)))).
- Sums: If (f_1(n)) is (O(g_1(n))) and ( f_2(n) ) is (O(g_2(n)))),then (f_1(n) + f_2(n)) is (O(max { g_1(n) , g_2(n) })).
- Transitivity: If (f(n)) is (O(g(n))) and ( g(n) ) is (O(h(n))),then ( f(n) ) is (O(h(n))).
- Polynomials: Let (f(n) = a_0 + a_1 n + ldots + a_d n^d) with(a_d > 0). Then, ( f(n) ) is (Theta(n^d)).
- Logarithms and polynomials: ( log_b n ) is (O(n^d)) for every ( b > 0) and every ( d > 0 ).
- Exponentials and polynomials: ( n^d ) is (O(r^n)) for every ( r > 0) and every ( d > 0 ).
- Factorials: ( n! ) is ( 2^{Theta(n log n)} ).
- Limits: If ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = c)for some constant ( 0 < c < infty), then(f(n)) is (Theta(g(n))).
- Limits: If ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = 0),then (f(n)) is (O(g(n))) but not (Theta(g(n))).
- Limits: If ( ; displaystyle lim_{n to infty} frac{f(n)}{g(n)} = infty),then (f(n)) is (Omega(g(n))) but not (O(g(n))).
Here are some examples.
| FUNCTION | (o(n^2)) | (O(n^2)) | (Theta(n^2)) | (Omega(n^2)) | (omega(n^2)) | (sim 2 n^2) | (sim 4 n^2) |
|---|---|---|---|---|---|---|---|
| (log_2 n) | ✔ | ✔ | |||||
| (10n + 45) | ✔ | ✔ | |||||
| (2n^2 + 45n + 12) | ✔ | ✔ | ✔ | ✔ | |||
| (4n^2 - 2 sqrt{n}) | ✔ | ✔ | ✔ | ✔ | |||
| (3n^3) | ✔ | ✔ | |||||
| (2^n) | ✔ | ✔ |
Divide-and-conquer recurrences.
For each of the following recurrences we assume (T(1) = 0)and that (n,/,2) means either (lfloor n,/,2 rfloor) or(lceil n,/,2 rceil).| RECURRENCE | (T(n)) | EXAMPLE |
|---|---|---|
| (T(n) = T(n,/,2) + 1) | (sim lg n) | binary search |
| (T(n) = 2 T(n,/,2) + n) | (sim n lg n) | mergesort |
| (T(n) = T(n-1) + n) | (sim frac{1}{2} n^2) | insertion sort |
| (T(n) = 2 T(n,/,2) + 1) | (sim n) | tree traversal |
| (T(n) = 2 T(n-1) + 1) | (sim 2^n) | towers of Hanoi |
| (T(n) = 3 T(n,/,2) + Theta(n)) | (Theta(n^{log_2 3}) = Theta(n^{1.58..})) | Karatsuba multiplication |
| (T(n) = 7 T(n,/,2) + Theta(n^2)) | (Theta(n^{log_2 7}) = Theta(n^{2.81..})) | Strassen multiplication |
| (T(n) = 2 T(n,/,2) + Theta(n log n)) | (Theta(n log^2 n)) | closest pair |
Master theorem.
Let (a ge 1), (b ge 2), and (c > 0) and suppose that(T(n)) is a function on the non-negative integers that satisfiesthe divide-and-conquer recurrence$$T(n) = a ; T(n,/,b) + Theta(n^c)$$with (T(0) = 0) and (T(1) = Theta(1)), where (n,/,b) meanseither (lfloor n,/,b rfloor) or either (lceil n,/,b rceil).- If (c < log_b a), then (T(n) = Theta(n^{log_{,b} a}))
- If (c = log_b a), then (T(n) = Theta(n^c log n))
- If (c > log_b a), then (T(n) = Theta(n^c))
Algorithm Complexity Cheat Sheet Pdf
Big-o Algorithm Complexity Cheat Sheet Pdf
Last modified on September 12, 2020.
Copyright © 2000–2019Robert SedgewickandKevin Wayne.All rights reserved.
